La manzana de Newton
Un año más tarde Newton fue inscrito en la King's School de la cercana población de Grantham. Hay testimonios de que en los años que allí pasó alojado en la casa del farmacéutico, se desarrolló su poco usual habilidad mecánica, que ejercitó en la construcción de diversos mecanismos (el más citado es un reloj de agua) y juguetes (las famosas cometas, a cuya cola ataba linternas que por las noches asustaban a sus convecinos). También se produjo un importante cambio en su carácter: su inicial indiferencia por los estudios, surgida probablemente de la timidez y el retraimiento, se cambió en feroz espíritu competitivo que le llevó a ser el primero de la clase, a raíz de una pelea con un compañero de la que salió vencedor.
Fue un muchacho «sobrio, silencioso, meditativo», que prefirió construir utensilios, para que las niñas jugaran con sus muñecas, a compartir las diversiones de los demás muchachos, según el testimonio de una de sus compañeras femeninas infantiles, quien, cuando ya era una anciana, se atribuyó una relación sentimental adolescente con Newton, la única que se le conoce con una mujer.
Cumplidos los dieciséis años, su madre lo hizo regresar a casa para que empezara a ocuparse de los asuntos de la heredad. Sin embargo, el joven Isaac no se mostró en absoluto interesado por asumir sus responsabilidades como terrateniente; su madre, aconsejada por el maestro de Newton y por su propio hermano, accedió a que regresara a la escuela para preparar su ingreso en la universidad.
Éste se produjo en junio de 1661, cuando Newton fue admitido en el Trinity College de Cambridge, y se matriculó como fámulo, ganando su manutención a cambio de servicios domésticos, pese a que su situación económica no parece que lo exigiera así. Allí empezó a recibir una educación convencional en los principios de la filosofía aristotélica (por aquel entonces, los centros que destacaban en materia de estudios científicos se hallaban en Oxford y Londres), pero en 1663 se despertó su interés por las cuestiones relativas a la investigación experimental de la naturaleza, que estudió por su cuenta.
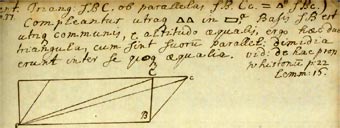
Manuscrito de Newton
Fruto de esos esfuerzos independientes fueron sus primeras notas acerca de lo que luego sería su cálculo de fluxiones, estimuladas quizá por algunas de las clases del matemático y teólogo Isaac Barrow; sin embargo, Newton hubo de ser examinado por Barrow en 1664 al aspirar a una beca y no consiguió entonces inspirarle ninguna opinión especialmente favorable.
Al declararse en Londres la gran epidemia de peste de 1665, Cambridge cerró sus puertas y Newton regresó a Woolsthorpe. En marzo de 1666 se reincorporó al Trinity, que de nuevo interrumpió sus actividades en junio al reaparecer la peste, y no reemprendió definitivamente sus estudios hasta abril de 1667. En una carta póstuma, el propio Newton describió los años de 1665 y 1666 como su «época más fecunda de invención», durante la cual «pensaba en las matemáticas y en la filosofía mucho más que en ningún otro tiempo desde entonces».
El método de fluxiones, la teoría de los colores y las primeras ideas sobre la atracción gravitatoria, relacionadas con la permanencia de la Luna en su órbita en torno a la Tierra, fueron los logros que Newton mencionó como fechados en esos años, y él mismo se encargó de propagar, también hacia el final de su vida, la anécdota que relaciona sus primeros pensamientos sobre la ley de la gravedad con la observación casual de una manzana cayendo de alguno de los frutales de su jardín (Voltaire fue el encargado de propagar en letra impresa la historia, que conocía por la sobrina de Newton).
La óptica
A su regreso definitivo a Cambridge, Newton fue elegido miembro becario del Trinity College en octubre de 1667, y dos años más tarde sucedió a Barrow en su cátedra. Durante sus primeros años de docencia no parece que las actividades lectivas supusieran ninguna carga para él, ya que tanto la complejidad del tema como el sistema docente tutorial favorecían el absentismo a las clases. Por esa época, Newton redactó sus primeras exposiciones sistemáticas del cálculo infinitesimal que no se publicaron hasta más tarde. En 1664 o 1665 había hallado la famosa fórmula para el desarrollo de la potencia de un binomio con un exponente cualquiera, entero o fraccionario, aunque no dio noticia escrita del descubrimiento hasta 1676, en dos cartas dirigidas a Henry Oldenburg, secretario de la Royal Society; el teorema lo publicó por vez primera en 1685 John Wallis, el más importante de los matemáticos ingleses inmediatamente anteriores a Newton, reconociendo debidamente la prioridad de este último en el hallazgo.
El procedimiento seguido por Newton para establecer la fórmula binomial tuvo la virtud de hacerle ver el interés de las series infinitas para el cálculo infinitesimal, legitimando así la intervención de los procesos infinitos en los razonamientos matemáticos y poniendo fin al rechazo tradicional de los mismos impuesto por la matemática griega. La primera exposición sustancial de su método de análisis matemático por medio de series infinitas la escribió Newton en 1669; Barrow conoció e hizo conocer el texto, y Newton recibió presiones encaminadas a que permitiera su publicación, pese a lo cual (o quizá precisamente por ello) el escrito no llegó a imprimirse hasta 1711.
Tampoco en las aulas divulgó Newton sus resultados matemáticos, que parece haber considerado más como una herramienta para el estudio de la naturaleza que como un tema merecedor de atención en sí; el capítulo de la ciencia que eligió tratar en sus clases fue la óptica, a la que venía dedicando su atención desde que en 1666 tuviera la idea que hubo de llevarle a su descubrimiento de la naturaleza compuesta de la luz. En febrero de 1672 presentó a la Royal Society su primera comunicación sobre el tema, pocos días después de que dicha sociedad lo hubiera elegido como uno de sus miembros en reconocimiento de su construcción de un telescopio reflector. La comunicación de Newton aportaba la indiscutible evidencia experimental de que la luz blanca era una mezcla de rayos de diferentes colores, caracterizado cada uno por su distinta refrangibilidad al atravesar un prisma óptico.
Réplica del telescopio de Newton
Newton consideró, con justicia, que su descubrimiento era «el más singular, cuando no el más importante, de los que se han hecho hasta ahora relativos al funcionamiento de la naturaleza». Pero sus consecuencias inmediatas fueron las de marcar el inicio de cuatro años durante los que, como él mismo le escribió a Leibniz en diciembre de 1675, «me vi tan acosado por las discusiones suscitadas a raíz de la publicación de mi teoría sobre la luz, que maldije mi imprudencia por apartarme de las considerables ventajas de mi silencio para correr tras una sombra».
El contraste entre la obstinación con que Newton defendió su primacía intelectual allí donde correspondía que le fuese reconocida (admitiendo sólo a regañadientes que otros pudieran habérsele anticipado) y su retraimiento innato que siempre le hizo ver con desconfianza la posibilidad de haberse de mezclar con el común de los mortales, es uno de los rasgos de su biografía que mejor parecen justificar la caracterización de su temperamento como neurótico; un diagnóstico que la existencia de sus traumas infantiles no ha hecho más que abonar, y que ha encontrado su confirmación en otras componentes de su personalidad como la hipocondría o la misoginia.
Los Principia
El primero en oponerse a las ideas de Newton en materia de óptica fue Robert Hooke, a quien la Royal Society encargó que informara acerca de la teoría presentada por aquél. Hooke defendía una concepción ondulatoria de la luz, frente a las ideas de Newton, precisadas en una nueva comunicación de 1675 que hacían de la luz un fenómeno resultante de la emisión de corpúsculos luminosos por parte de determinados cuerpos. La acritud de la polémica determinó que Newton renunciara a publicar un tratado que contuviera los resultados de sus investigaciones hasta después de la muerte de Hooke y, en efecto, su Opticks no se publicó hasta 1704. Por entonces, la obra máxima de Newton había ya visto la luz.
En 1676 Newton renunció a proseguir la polémica acerca de su teoría de los colores y por unos años, se refugió de nuevo en la intimidad de sus trabajos sobre el cálculo diferencial y en su interés (no por privado, menos intenso) por dos temas aparentemente alejados del mundo sobrio de sus investigaciones sobre la naturaleza: la alquimia y los estudios bíblicos. La afición de Newton por la alquimia (John Maynard Keynes lo llamó «el último de los magos») estaba en sintonía con su empeño por trascender el mecanicismo de observancia estrictamente cartesiana que todo lo reducía a materia y movimiento y llegar a establecer la presencia efectiva de lo espiritual en las operaciones de la naturaleza.
Newton no concebía el cosmos como la creación de un Dios que se había limitado a legislarlo para luego ausentarse de él, sino como el ámbito donde la voluntad divina habitaba y se hacía presente, imbuyendo en los átomos que integraban el mundo un espíritu que era el mismo para todas las cosas y que hacía posible pensar en la existencia de un único principio general de orden cósmico. Y esa búsqueda de la unidad en la naturaleza por parte de Newton fue paralela a su persecución de la verdad originaria a través de las Sagradas Escrituras, persecución que hizo de él un convencido antitrinitario y que seguramente influyó en sus esfuerzos hasta conseguir la dispensa real de la obligación de recibir las órdenes sagradas para mantener su posición en el Trinity College.
Traducción italiana de los Principia
En 1679 Newton se ausentó de Cambridge durante varios meses con motivo de la muerte de su madre, y a su regreso en el mes de noviembre, recibió una carta de Hooke, por entonces secretario de la Royal Society, en la que éste trataba de que Newton restableciera su contacto con la institución y le sugería la posibilidad de hacerlo comentando las teorías del propio Hooke acerca del movimiento de los planetas. Como resultado, Newton reemprendió una correspondencia sobre el tema que, con el tiempo, habría de desembocar en reclamaciones de prioridad para Hooke en la formulación de la ley de la atracción gravitatoria; por el momento, su efecto fue el de devolverle a Newton su interés por la dinámica y hacerle ver que la trayectoria seguida por un cuerpo que se moviera bajo el efecto de una fuerza inversamente proporcional al cuadrado de las distancias, tendría forma elíptica (y no sería una espiral, como él creyó en principio, dando pie a ser corregido por Hooke).
Cuando cinco años más tarde Edmond Halley, quien por entonces había ya observado el cometa que luego llevó su nombre, visitó a Newton en Cambridge y le preguntó cuál sería la órbita de un planeta si la gravedad disminuyese con el cuadrado de la distancia, su respuesta fue inmediata: una elipse. Maravillado por la rapidez con que Newton consideraba resuelto un asunto en cuyo esclarecimiento andaban compitiendo desde hacía varios meses Hooke y el propio Halley, éste inquirió cómo podía conocer Newton la forma de la curva y obtuvo una contestación tajante: «La he calculado». La distancia que iba entre el atisbo de una verdad y su demostración por el cálculo marcaba la diferencia fundamental entre Hooke y Newton, a la par que iluminaba s
obre el sentido que este último daría a su insistente afirmación de «no fingir hipótesis».
Newton según el visionario pintor William Blake
Sin embargo, en aquel día del verano de 1684 Newton no pudo encontrar sus cálculos para mostrárselos a Halley, y éste tuvo que conformarse con la promesa de que le serían enviados una vez rehechos. La reconstrucción, empero, chocó con un obstáculo: demostrar que la fuerza de atracción entre dos esferas es igual a la que existiría si las masas de cada una de ellas estuviesen concentradas en los centros respectivos. Newton resolvió ese problema en febrero de 1685, tras comprobar la validez de su ley de la atracción gravitatoria mediante su aplicación al caso de la Luna; la idea, nacida veinte años antes, quedó confirmada entonces merced a la medición precisa del radio de la Tierra realizada por el astrónomo francés Jean Picard.
El camino quedaba abierto para reunir todos los resultados en un tratado sobre la ciencia del movimiento: losPhilosophiae naturalis principia mathematica (Los principios matemáticos de la filosofía natural). La intervención de Halley en la publicación de la obra no se limitó a la de haber sabido convencer a su autor de consentir en ella, algo ya muy meritorio tratándose de Newton; Halley supo capear el temporal de la polémica con Hooke, se encargó de que el manuscrito fuese presentado en abril de 1686 ante la Royal Society y de que ésta asumiera su edición, para acabar corriendo personalmente con los gastos de la impresión, terminada en julio de 1687.
De Cambridge a Londres
Los Principia contenían la primera exposición impresa del cálculo infinitesimal creado por Newton, aunque éste prefirió que, en general, la obra presentara los fundamentos de la física y la astronomía formulados en el lenguaje sintético de la geometría. Newton no fue el primero en servirse de aquel tipo de cálculo; de hecho, la primera edición de su obra contenía el reconocimiento de que Leibniz estaba en posesión de un método análogo. Sin embargo, la disputa de prioridades en que se enzarzaron los partidarios de uno y otro determinó que Newton suprimiera la referencia a Leibniz en la tercera edición de 1726. El detonante de la polémica (orquestada por el propio Newton entre bastidores) lo constituyó la insinuación de que Leibniz podía haber cometido plagio, expresada en 1699 por Nicolas Fatio de Duillier, un matemático suizo admirador de Newton, con el que mantuvo una íntima amistad de 1689 a 1693.
Ese año Newton atravesó por una crisis paranoica de la que se ha tratado de dar diversas explicaciones, entre las que no ha faltado, desde luego, la consistente en atribuirla a la ruptura de su relación con el joven Fatio, relación que, por otra parte, no parece que llevara a Newton a traspasar las férreas barreras de su código moral puritano. Los contemporáneos de Newton popularizaron la improbable explicación de su trastorno como consecuencia de que algunos de sus manuscritos resultaran destruidos en un incendio; más recientemente se ha hablado de una lenta y progresiva intoxicación derivada de sus experimentos alquímicos con mercurio y plomo. Por fin, no pueden olvidarse como causa plausible de la depresión las dificultades que Newton encontró para conseguir un reconocimiento público más allá del estricto ámbito de la ciencia, reconocimiento que su soberbia exigía y cuya ausencia no podía interpretar sino como resultado de una conspiración de la historia.
Pese a la dificultad de su lectura, los Principia le habían hecho famoso en la comunidad científica y Newton había formado parte en 1687 de la comisión que la Universidad de Cambridge envió a Londres para oponerse a las medidas de catolización del rey Jacobo II. Aunque quizá su intervención se debió más a su condición de laico que a su fama, ello le valió ser elegido por la universidad como representante suyo en el parlamento formado como consecuencia del desembarco de Guillermo de Orange y el exilio de Jacobo II a finales de 1688.
Su actividad parlamentaria, que duró hasta febrero de 1690, se desarrolló en estrecha colaboración con Charles Montagu, más tarde lord Halifax, a quien había conocido pocos años antes como alumno en Cambridge y que fue el encargado de dar cumplimiento a los deseos de Newton de cambiar su retiro académico en Cambridge por la vida pública en Londres. Montagu fue nombrado canciller de la hacienda real en abril de 1694; cuando su ley de reacuñación fue aprobada en 1695, le otorgó a Newton el cargo de inspector de la Casa de la Moneda, siendo ascendido al de director en 1699. Lord Halifax acabó por convertirse en el amante de la sobrina de Newton, aunque los cargos obtenidos por éste, pese a las acusaciones lanzadas por Voltaire, no tuvieron que ver con el asunto.
Busto de Newton
A fines de 1701 Newton fue elegido de nuevo miembro del parlamento como representante de su universidad, pero poco después renunció definitivamente a su cátedra y a su condición de fellow del Trinity College, confirmando así un alejamiento de la actividad científica que se remontaba, de hecho, a su llegada a Londres. En 1703, tras la muerte de Hooke y una vez que el final de la reacuñación había devuelto la tranquilidad de una sinecura a la dirección de la Casa de la Moneda, Newton fue elegido presidente de la Royal Society, cargo que conservó hasta su muerte. En 1705 se le otorgó el título de sir. Pese a su hipocondría, alimentada desde la infancia por su condición de niño prematuro, Newton gozó de buena salud hasta los últimos años de su vida; a principios de 1722 una afección renal lo tuvo seriamente enfermo durante varios meses y en 1724 se produjo un nuevo cólico nefrítico. En los primeros días de marzo de 1727 el alojamiento de otro cálculo en la vejiga marcó el comienzo de su agonía: Newton murió en la madrugada del 20 de marzo, tras haberse negado a recibir los auxilios finales de la Iglesia, consecuente con su aborrecimiento del dogma de la Trinidad.